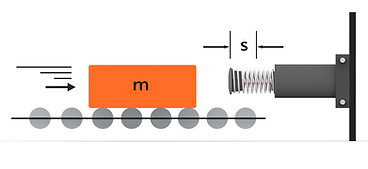
CALCULATION CONCEPTS 

​

• Kinetic Energy (W1): The energy possessed by a moving mass due to its velocity.

  • Formula: W1 = 1/2 * m * v^2

  • Significance: This is the primary energy that the shock absorber must dissipate to bring the moving mass to a complete stop.

​

• Total Energy Per Stroke (W3): In the absence of external propelling forces, the total energy to be absorbed by the shock absorber is equal to the kinetic energy of the moving mass.

  • Formula: W3 = W1 + W2 (where W2 = 0 for no propelling force)

​

• Load Factor: The ratio of the total energy per stroke (W3) to the shock absorber's maximum allowable energy capacity.

  • Formula: Load Factor = (W3 / W3per) * 100

  • Recommendation: For optimal performance and durability, the load factor should ideally be below 80%.

​

• Impact Speed (vD): The velocity of the mass at the moment of impact with the shock absorber. In this case, it is equal to the initial velocity of the moving mass (v).

​

• Effective Mass (me): The equivalent mass experienced by the shock absorber during deceleration. It ensures smooth deceleration over the entire stroke length.

  • Formula: me = W3 / (1/2 * v^2)

  • Note: The effective mass must fall within the shock absorber's specified permissible range.

​

• Deceleration Time (t): The time required to bring the moving mass to a complete stop.

  • Approximate Formula: t ≈ 2.6 * s / vD

  • Note: Shorter deceleration times generally result in higher forces on the shock absorber.

​

• Supporting Force (Q): The force exerted by the shock absorber to decelerate the mass.

  • Formula: Q = 1.5 * W3 / s

  • Note: The structure to which the shock absorber is mounted must be adequately designed to withstand this force.

​

• Cycles Per Hour (x): The number of impacts the shock absorber experiences within one hour.

  • Formula: x = 3600 / (t_reset + t)

  • Note: The actual number of cycles per hour must not exceed the shock absorber's maximum permissible cycles per hour (xper).

​​

​

SIZING PROCEDURE

​

1. Gather Input Data:

   • Mass of the object (m) in kilograms

   • Velocity at impact (v) in meters per second

   • Desired stroke length (s) in meters

   • Number of cycles per hour (x) in impacts/hour

2. Calculate Total Energy Per Stroke (W3): Use the formula W3 = 1/2 * m * v^2

3. Determine Effective Mass (me): Calculate me using the formula me = W3 / (1/2 * v^2) and ensure it falls within the acceptable range for the shock absorber.

4. Estimate Deceleration Time (t): Calculate t using the approximate formula t ≈ 2.6 * s / vD.

5. Verify Supporting Force (Q): Calculate Q using the formula Q = 1.5 * W3 / s and ensure the mounting structure can withstand this force.

6. Check Load Factor and Cycles Per Hour:

   • Calculate the Load Factor and ensure it is below 80% for optimal performance.

   • Verify that the actual cycles per hour (x) do not exceed the maximum permissible cycles per hour (xper) for the shock absorber.

​

Example Calculation

• Given:

  • Mass (m) = 100 kg

  • Velocity (v) = 3 m/s

  • Stroke Length (s) = 0.3 m

​

• Step 1: Calculate W3:

  • W3 = 1/2 * 100 kg * (3 m/s)^2 = 450 Nm

​

• Step 2: Determine me:

  • me = 450 Nm / (1/2 * (3 m/s)^2) = 100 kg

​

• Step 3: Estimate t:

  • t ≈ 2.6 * 0.3 m / 3 m/s = 0.26 s

​

• Step 4: Verify Q:

  • Q = 1.5 * 450 Nm / 0.3 m = 2250 N

​

Note: This is a simplified guide. For precise sizing, consider factors like operating temperature, environmental conditions, and specific shock absorber characteristics.

​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​